Hyperparameters selection with 1-std rule

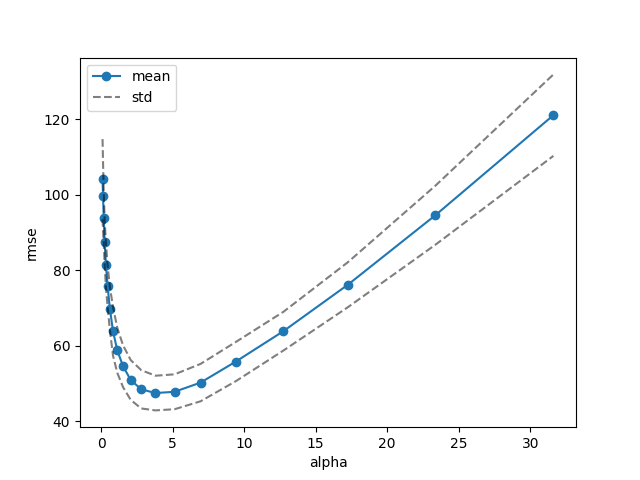
One-standard-deviation rule is a technique to promote model robustness when cross validation results are noisy. The hyperparameter is chosen to be equal to the maximum value that yields:

CV = minimum CV + 1 * std(CV at minimum).

One-standard-deviation rule is available in both GridSearchCV and LineSearchCV under sparselm.model_selection.

• 
• 

Lasso with 1-std:
    alpha value: 6.9519279617756045
    train r2: 0.957
    test r2: 0.941
    train rmse: 44.083
    test rmse: 47.177
    sparsity: 13
Lasso performance:
    alpha value: 6.9519279617756045
    train r2: 0.968
    test r2: 0.952
    train rmse: 37.854
    test rmse: 42.665
    sparsity: 22

import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import make_regression
from sklearn.linear_model import Lasso
from sklearn.metrics import mean_squared_error, r2_score
from sklearn.model_selection import KFold, train_test_split

from sparselm.model_selection import GridSearchCV

X, y, coef = make_regression(
    n_samples=200,
    n_features=100,
    n_informative=10,
    noise=40.0,
    bias=-15.0,
    coef=True,
    random_state=0,
)

X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.25, random_state=0
)

# create estimators
lasso = Lasso(fit_intercept=True)

# create cv search objects for each estimator
cv5 = KFold(n_splits=5, shuffle=True, random_state=0)
params = {"alpha": np.logspace(-1, 1.5, 20)}

lasso_cv_std = GridSearchCV(
    lasso, params, opt_selection_method="one_std_score", cv=cv5, n_jobs=-1
)
lasso_cv_opt = GridSearchCV(
    lasso, params, opt_selection_method="max_score", cv=cv5, n_jobs=-1
)

# fit models on training data
lasso_cv_std.fit(X_train, y_train)
lasso_cv_opt.fit(X_train, y_train)

# calculate model performance on test and train data
lasso_std_train = {
    "r2": r2_score(y_train, lasso_cv_std.predict(X_train)),
    "rmse": np.sqrt(mean_squared_error(y_train, lasso_cv_std.predict(X_train))),
}

lasso_std_test = {
    "r2": r2_score(y_test, lasso_cv_std.predict(X_test)),
    "rmse": np.sqrt(mean_squared_error(y_test, lasso_cv_std.predict(X_test))),
}

print("Lasso with 1-std:")
print(f"    alpha value: {lasso_cv_std.best_params_['alpha']}")
print(f"    train r2: {lasso_std_train['r2']:.3f}")
print(f"    test r2: {lasso_std_test['r2']:.3f}")
print(f"    train rmse: {lasso_std_train['rmse']:.3f}")
print(f"    test rmse: {lasso_std_test['rmse']:.3f}")
print(f"    sparsity: {sum(abs(lasso_cv_std.best_estimator_.coef_) > 1E-8)}")

lasso_opt_train = {
    "r2": r2_score(y_train, lasso_cv_opt.predict(X_train)),
    "rmse": np.sqrt(mean_squared_error(y_train, lasso_cv_opt.predict(X_train))),
}

lasso_opt_test = {
    "r2": r2_score(y_test, lasso_cv_opt.predict(X_test)),
    "rmse": np.sqrt(mean_squared_error(y_test, lasso_cv_opt.predict(X_test))),
}

print("Lasso performance:")
print(f"    alpha value: {lasso_cv_std.best_params_['alpha']}")
print(f"    train r2: {lasso_opt_train['r2']:.3f}")
print(f"    test r2: {lasso_opt_test['r2']:.3f}")
print(f"    train rmse: {lasso_opt_train['rmse']:.3f}")
print(f"    test rmse: {lasso_opt_test['rmse']:.3f}")
print(f"    sparsity: {sum(abs(lasso_cv_opt.best_estimator_.coef_) > 1E-8)}")

# plot cross validation scores
fig, ax = plt.subplots()
ax.plot(
    lasso_cv_std.cv_results_["param_alpha"].data,
    -lasso_cv_std.cv_results_["mean_test_score"],
    "o-",
    label="One std",
)
ax.plot(
    lasso_cv_std.cv_results_["param_alpha"].data,
    -lasso_cv_opt.cv_results_["mean_test_score"]
    + lasso_cv_std.cv_results_["std_test_score"],
    "k--",
    alpha=0.5,
)
ax.plot(
    lasso_cv_std.cv_results_["param_alpha"].data,
    -lasso_cv_opt.cv_results_["mean_test_score"]
    - lasso_cv_std.cv_results_["std_test_score"],
    "k--",
    alpha=0.5,
)
ax.set_xlabel("alpha")
ax.set_ylabel("rmse")
ax.legend(["mean", "std"])
fig.show()

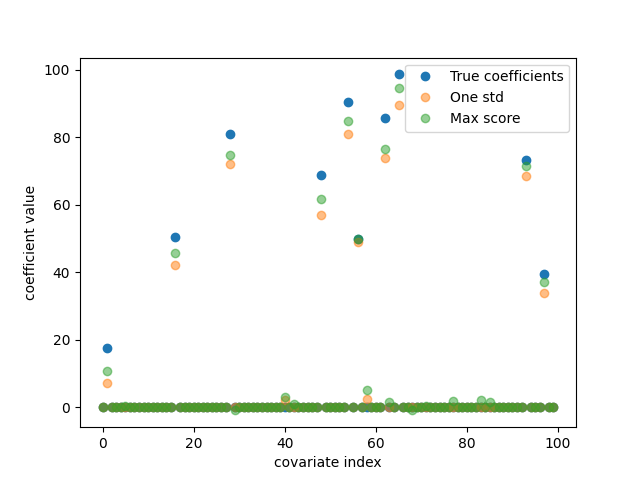
# plot model coefficients
fig, ax = plt.subplots()
ax.plot(coef, "o", label="True coefficients")
ax.plot(lasso_cv_std.best_estimator_.coef_, "o", label="One std", alpha=0.5)
ax.plot(lasso_cv_opt.best_estimator_.coef_, "o", label="Max score", alpha=0.5)
ax.set_xlabel("covariate index")
ax.set_ylabel("coefficient value")
ax.legend()
fig.show()