LiMnO DRX Cluster Expansion#
This example shows a more in depth example of how to generate, fit and sample a cluster expansion for a slightly more complex scenario.
0) Load all data#
Load the structures with oxidation state assignments and prepare the target vector for learning. Target vector is usually a vector of total energies.
[1]:
# load the training structures with oxidation state assigned
from monty.serialization import loadfn
entries = loadfn("data/lmo_drx_entries.json")
1) Define a cluster expansion#
Load and inspect the lattice primitive cell with multi-site disorder#
[2]:
prim = loadfn("data/lmo_drx_prim.json")
See that the primitive cell is randomly disordered. When occupancies on a site (#) do not add to 1, it means vacancies are considered.
[3]:
import crystal_toolkit
print(prim)
prim
Full Formula (Li0.7 Mn1.1 O1)
Reduced Formula: Li0.7Mn1.1O1
abc : 2.969850 2.969850 2.969850
angles: 60.000000 60.000000 60.000000
Overall Charge: +1.5
Sites (4)
# SP a b c
--- --------------------------------------------- ---- ---- ----
0 Li+:0.250, Mn2+:0.250 0.75 0.75 0.75
1 Li+:0.250, Mn2+:0.250 0.25 0.25 0.25
2 Li+:0.200, Mn2+:0.200, Mn3+:0.200, Mn4+:0.200 0 0 0
3 O2- 0.5 0.5 0.5
If you see this text, the Crystal Toolkit Jupyter Lab
extension is not installed. You can install it by running
"pip install crystaltoolkit-extension"
from the same environment you run "jupyter lab".
This only works in Jupyter Lab 3.x or above.
Structure Summary
Lattice
abc : 2.96985 2.9698500000000005 2.96985
angles : 60.00000000000001 59.99999999999999 60.00000000000001
volume : 18.522028420882272
A : 2.571965545429215 0.0 1.4849250000000003
B : 0.8573218484764051 2.4248723708682074 1.4849250000000003
C : 0.0 0.0 2.96985
Overall Charge: +1.5
PeriodicSite: Li+:0.250, Mn2+:0.250 (2.5720, 1.8187, 4.4548) [0.7500, 0.7500, 0.7500]
PeriodicSite: Li+:0.250, Mn2+:0.250 (0.8573, 0.6062, 1.4849) [0.2500, 0.2500, 0.2500]
PeriodicSite: Li+:0.200, Mn2+:0.200, Mn3+:0.200, Mn4+:0.200 (0.0000, 0.0000, 0.0000) [0.0000, 0.0000, 0.0000]
PeriodicSite: O2- (1.7146, 1.2124, 2.9699) [0.5000, 0.5000, 0.5000]
Specify cluster subspace information#
We will include an electrostatic term in the subspace as well
[4]:
from smol.cofe import ClusterSubspace
from smol.cofe.extern import EwaldTerm
CLUSTERCUTOFFS = {2: 6, 3: 4, 4:2}
LTOL, STOL, ATOL = 0.15, 0.20, 15
BASIS = 'sinusoid'
cs = ClusterSubspace.from_cutoffs(structure=prim,
cutoffs = CLUSTERCUTOFFS,
ltol = LTOL,
stol = STOL,
angle_tol = ATOL,
supercell_size = ('O2-'),
basis = BASIS,
orthonormal=False)
cs.add_external_term(EwaldTerm())
Print some information about the subspace, such as the number of correlation functions for the random structure \(\langle \Phi_\beta \rangle\), number of function clusters \(\alpha\), number of orbits \(\textbf{B}\), and the orbit ids for all correlation functions \(B\) which describes how correlation functions are grouped together.
[5]:
print(cs)
Basis/Orthogonal/Orthonormal : sinusoid/True/{self.basis_orthonormal}
Unit Cell Composition : Li+0.7 Mn2+0.7 Mn3+0.2 Mn4+0.2 O2-1
Number of Orbits : 40
No. of Correlation Functions : 386
Cluster Cutoffs : 2: 5.94, 3: 3.64
External Terms : [EwaldTerm(total)]
Orbit Summary
------------------------------------------------------------------------
| ID Degree Cluster Diameter Multiplicity No. Functions |
| 0 0 NA 0 1 |
| 1 1 0.0000 2 2 |
| 2 1 0.0000 1 4 |
| 3 2 1.8187 8 8 |
| 4 2 2.1000 6 3 |
| 5 2 2.9698 12 3 |
| 6 2 2.9699 6 10 |
| 7 2 3.4825 24 8 |
| 8 2 3.6373 4 3 |
| 9 2 3.6373 4 3 |
| 10 2 4.2000 6 3 |
| 11 2 4.2000 3 10 |
| 12 2 4.5768 24 8 |
| 13 2 4.6957 24 3 |
| 14 2 5.1439 24 4 |
| 15 2 5.1439 12 10 |
| 16 2 5.4560 24 8 |
| 17 2 5.4560 8 8 |
| 18 2 5.9397 12 3 |
| 19 2 5.9397 6 10 |
| 20 3 2.1000 12 12 |
| 21 3 2.9699 24 6 |
| 22 3 2.9699 12 12 |
| 23 3 2.9699 12 20 |
| 24 3 2.9699 8 4 |
| 25 3 2.9699 8 4 |
| 26 3 2.9699 8 20 |
| 27 3 3.4825 48 32 |
| 28 3 3.4825 48 16 |
| 29 3 3.4825 24 16 |
| 30 3 3.4825 24 12 |
| 31 3 3.4825 24 12 |
| 32 3 3.4825 24 20 |
| 33 3 3.4825 12 12 |
| 34 3 3.4825 12 20 |
| 35 3 3.6373 24 16 |
| 36 3 3.6373 24 8 |
| 37 3 3.6373 24 8 |
| 38 3 3.6373 24 12 |
| 39 3 3.6373 4 12 |
------------------------------------------------------------------------
Load structure data into the StructureWrangler, which is used later for fitting
[6]:
from smol.cofe import StructureWrangler
sw = StructureWrangler(cs)
for entry in entries:
sw.add_entry(entry, verbose=False)
This next step may take a few minutes to complete.
Our final feature matrix for fitting has shape \(n \times p\) where \(n\) is the number of structures and \(p\) is the number of correlation functions for our training structure and the Ewald energy.
[7]:
print ('Our feature matrix has the following dimensions:',
sw.feature_matrix.shape)
Our feature matrix has the following dimensions: (238, 387)
2. Fit a cluster expansion#
Here we are fitting $E(\sigma) = \sum:nbsphinx-math:`beta `m\beta `J\_:nbsphinx-math:beta :nbsphinx-math:langle :nbsphinx-math:Phi (:nbsphinx-math:sigma`):nbsphinx-math:`alpha `:nbsphinx-math:`rangle`\beta `+ :nbsphinx-math:frac{1}{epsilon}`E_{Ewald}(\sigma) $ and we will do with various compressive sensing techniques because the system is under-determined because \(n\) < \(p\). Our feature matrix \(\textbf{X}\) is the matrix of all correlation functions and Ewald energy for our structures. We are interested in finding $ m_:nbsphinx-math:beta `J_:nbsphinx-math:beta`$ and \(\frac{1}{\epsilon}\) which together form vector \(\vec w\).
[8]:
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error as mse
import numpy as np
import copy
We will use L1-regularization, which is to minimize the following objective function with a penalty parameter \(\lambda\) (note that in sklearn this is called \(\alpha\), but we have already used this to define our function cluster). \begin{equation} \frac{1}{2n}||E-\textbf{X}\vec w||_2^2 + \lambda ||\vec w||_1 \end{equation}
We will optimize the hyperparameter using only a single fit with a train/test split. However, improved results can be obtained from doing a proper cross validation optimization.
[9]:
import warnings
from sklearn.linear_model import Lasso
from sklearn.exceptions import ConvergenceWarning
TRIALS = 50
TEST_SIZE = 0.20
PROPERTY = 'energy'
# we will suppress convergence warnings for now
with warnings.catch_warnings():
warnings.filterwarnings("ignore", category=ConvergenceWarning)
all_rmse = []
for alpha in np.logspace(-5, -3):
rmse_list = []
for _ in range(TRIALS):
X_train, X_test, y_train, y_test = train_test_split(
sw.feature_matrix, sw.get_property_vector(key=PROPERTY),
test_size=TEST_SIZE
)
model = Lasso(alpha=alpha, fit_intercept=True)
# remove the constant correlation since we are fitting
# the intercept
model.fit(X_train[:, 1:], y_train)
wvec = np.concatenate((np.array([model.intercept_]),
model.coef_),
axis=0)
y_predict = np.dot(X_test, wvec)
rmse = np.sqrt(mse(y_test, y_predict))
rmse_list.append(rmse)
all_rmse.append(np.mean(rmse_list))
Load plotting tools to examine how the fitting is going.
[11]:
import matplotlib as mpl
import matplotlib.pyplot as plt
%matplotlib inline
plt.scatter(np.logspace(-5,-2), all_rmse)
plt.xlim([0, 0.0009])
plt.axvline(x = 0.0002, ls = '--', color = 'black')
plt.xlabel(r'Penalty hyper-parameter $\alpha$')
plt.ylabel('Average RMSE (eV/prim) in 50 trials')
[11]:
Text(0, 0.5, 'Average RMSE (eV/prim) in 50 trials')
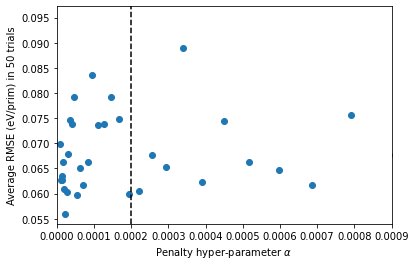
Although we sampled a large space of penalties, \(10^{-5}\) to \(10^{-2}\), it turns out that the relevant space of hyperparameters is \(10^{-5}\) to \(10^{-4}\).
We choose the penalty of \(\lambda=0.0002\) as the regularization parameter. So, we settle on our final model and show the out-of-sample and in-sample RMSE.
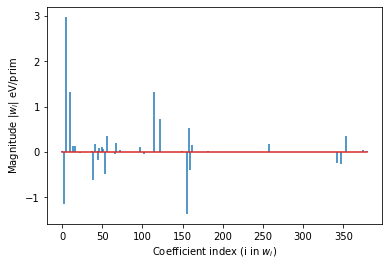
The weights \(\vec w\) are also plotted.
[12]:
LAMBDA = 0.0002
X_train, X_test, y_train, y_test = train_test_split(
sw.feature_matrix, sw.get_property_vector(key=PROPERTY),
test_size=TEST_SIZE
)
model = Lasso(alpha=LAMBDA, fit_intercept=True)
model.fit(X_train[:, 1:], y_train)
wvec = np.concatenate(
(np.array([model.intercept_]), model.coef_),
axis=0
)
y_predict = np.dot(X_test, wvec)
y_train_predict = np.dot(X_train, wvec)
print(f'Out-of-sample RMSE is: {np.sqrt(mse(y_test, y_predict))} eV/prim')
print(f'In-sample RMSE is: {np.sqrt(mse(y_train, y_train_predict))} eV/prim')
print(f'Number of Features > 1E-5: {sum(np.abs(wvec) > 1E-5)}/{len(wvec)}')
first_pair = cs.orbits_by_size[2][0].bit_id
print(f'Point correlation coefficients: {wvec[:first_pair]}')
# plot the coefficients (excluding those for points))
plt.stem(range(len(wvec) - first_pair), wvec[first_pair:],
linefmt='-', markerfmt=' ')#, basefmt=' ')
plt.xlabel('Coefficient index (i in $w_i$)')
plt.ylabel('Magnitude |$w_i$| eV/prim')
Out-of-sample RMSE is: 0.1542109191827612 eV/prim
In-sample RMSE is: 0.02426213156609966 eV/prim
Number of Features > 1E-5: 41/387
Point correlation coefficients: [-20.88771952 -2.04993158 0. 0. 1.18082107
-1.78346928 0. ]
/home/lbluque/miniconda3/envs/matx_dev/lib/python3.8/site-packages/sklearn/linear_model/_coordinate_descent.py:530: ConvergenceWarning: Objective did not converge. You might want to increase the number of iterations. Duality gap: 0.16306747608609712, tolerance: 0.05853817658209538
model = cd_fast.enet_coordinate_descent(
[12]:
Text(0, 0.5, 'Magnitude |$w_i$| eV/prim')
Generate the Cluster Expansion object#
[13]:
from smol.cofe import RegressionData, ClusterExpansion
from random import choice
reg_data = RegressionData.from_sklearn(
model, sw.feature_matrix, sw.get_property_vector(key=PROPERTY)
)
expansion = ClusterExpansion(
cs, coefficients=wvec, regression_data=reg_data
)
structure = choice(sw.structures)
prediction = expansion.predict(structure, normalize=True)
print(f"Structure with composition {structure.composition} has predicted energy {prediction} eV/prim")
Structure with composition Li+10 Mn4+12 Mn3+2 O2-32 has predicted energy -18.959213889450854 eV/prim
3) Run Canonical Monte Carlo#
Now let’s run a canonical MC disordering of spinel LiMn2O4.
First load the spinel structure#
[14]:
# load the spinel structure first and determine its supercell matrix
spinel = loadfn('data/LiMn2O4_drx_tutorial.json')
starting_matrix = sw.cluster_subspace.scmatrix_from_structure(spinel)
Generate an ensemble for a given transformation of the starting spinel structure and convert the spinel structure into an initial occupancy#
[15]:
from smol.moca import Ensemble
from smol.moca import Sampler
transformation = np.matrix([[3, 0, 0], [0, 3, 0], [0, 0, 3]])
sc_matrix = starting_matrix @ transformation
# Create an Ensemble as
ensemble = Ensemble.from_cluster_expansion(expansion, sc_matrix)
# Since computing the Ewald matrix is very time consuming make sure to
# save/load the ensemble or processor
# ensemble = dumpfn(ensemble, "data/lmo_drx_ensemble.json")
spinel = spinel.__mul__(transformation)
init_occu = ensemble.processor.occupancy_from_structure(spinel)
Generate sampler for canonical MC disordering from \(T_0 = 300 K\) to \(T_f = 500 K\) in steps of \(50 K\) as a mini simulation#
Computing the ewald matrix necessary for fast MC evaluation for large supercells with multi-component structures such as this example can take a long time. Since this is done lazily in the code it will seem like the first step of MC is unbearibly long. It is suggested to save the ensemble or processor used such that the Ewald matrix does not need to be reconstructed at runtime.
[16]:
from smol.moca import Sampler
T0 = 300
TF = 500
STEP = 50
PROPOSALS = int(1E5)
current_occu = None
save_data = {}
for T in range(T0, TF + 1, STEP):
sampler = Sampler.from_ensemble(ensemble=ensemble,
kernel_type='Metropolis',
temperature=T)
if current_occu is None:
current_occu = init_occu
sampler.run(PROPOSALS,
initial_occupancies=current_occu,
thin_by=100,
progress=True)
current_occu = sampler.samples.get_occupancies()[-1]
# now save some data such as occupancies
save_data[int(T)] = {'occupancies': sampler.samples.get_occupancies(),
'energies_total': sampler.samples.get_energies(),
'features_unnormalized': sampler.samples.get_feature_vectors()}
Sampling 1 chain(s) from a cell with 3456 sites...: 100%|██████████| 100000/100000 [00:53<00:00, 1873.63it/s]
Sampling 1 chain(s) from a cell with 3456 sites...: 100%|██████████| 100000/100000 [00:51<00:00, 1947.93it/s]
Sampling 1 chain(s) from a cell with 3456 sites...: 100%|██████████| 100000/100000 [00:51<00:00, 1950.93it/s]
Sampling 1 chain(s) from a cell with 3456 sites...: 100%|██████████| 100000/100000 [00:51<00:00, 1955.61it/s]
Sampling 1 chain(s) from a cell with 3456 sites...: 100%|██████████| 100000/100000 [00:51<00:00, 1956.76it/s]
Now save the data#
[ ]:
from monty.serialization import dumpfn
filename = "canonical_MC_LiMn2O4_{}_{}_{}.json".format(T0, TF, STEP)
dumpfn(save_data, filename)
